Tag Archives: quantum mechanics

High thermal conductivity of amorphous silicon – a quantum mechanics size effect?

Posted on by

High thermal conductivity of 80 micron thick a-Si film

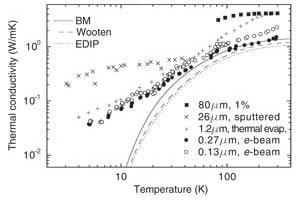
Higher conductivity of amorphous silicon (a-Si) found in 80 micron samples compared to submicron samples thought to be depend on the mean free path of phonons is negated by the size effect of quantum mechanics

Background
Thermoreflectance (TDTR) measurements at room temperature for an 80 micron a-Si sample show at more than a 2-fold increase in thermal conductivity compared to submicron samples having thicknesses of 200 nm and between 1 and 2 microns. See Yang et al., “Anomalously high thermal conductivity of amorphous Si deposited by hot wire chemical vapor deposition,” March, 2010. http://users.mrl.uiuc.edu/cahill/asi_v3.pdf On this basis, it was concluded: (1) phonons with a mean free path of ~ 100 nm make a sizeable contribution to conductivity, (2) size in terms of the sample thickness was not expected to make a significant difference in measured conductivity for the 80 micron and 200 nm samples, and (3) current theoretical methods cannot account for the nearly 40 percent contribution from phonons with a mean free path between 100 to 600 nm as inferred from the TDTR measurements. See http://cdac.ciw.edu/component/content/250.html?task=view

Problem and Hypothesis
Heat conduction based on atomic vibrations by Debye’s phonons has served well at the macroscale, but not in comparisons with experiment at the nanoscale. Like the difficulty in explaining the higher conductivity in the 80 micron samples, agreement if any is found by hand waving” the phonon wavelength that agrees with experiment, e.g., minimum thermal conductivity where the Boltzmann equation is used with the mean free path set to a “lattice” constant, to a “fracton” model in which heat is transported by anharmonically assisted hopping of localized vibrations, to diffusion-like conduction, with heat transported mainly by extended states but which do not have “good” wavelengths. Ibid.  The question may be asked:

Are phonons the mechanism of heat transfer at the nanoscale?

Alternatively, is the size effect of quantum mechanics at play in extending the validity of classical heat transfer at the macroscale to the nanoscale. But there are more basic questions:

At the nanoscale, does heat conduction even exist?

Indeed, if there is no conduction, calculations of thermal conductivity based on phonons are meaningless thereby avoiding the “hand-waving” of wavelengths to explain experiments. But if so, the remaining question is:

What is the heat transfer mechanism at the nanoscale?

If a heat transfer mechanism at the nanoscale is hypothesized that promptly conserves absorbed heat without any need to include conductive heat flow, the difficulties in explaining experiments by phonon wavelengths would be avoided. Bulk conductivity could then be assumed at the nanoscale even though there is no heat flow. Indeed, if such a heat transfer mechanism can be shown to exist, then all the above questions are answered.

QED induced EM radiation
One such heat transfer mechanism at the nanoscale that avoids phonons is the theory of QED induced EM radiation. QED stands for quantum electrodynamics and EM for electromagnetic. By this theory, absorbed EM is promptly conserved by the QED induced creation of photons within the nanostructure that then are emitted to the surroundings as non-thermal QED radiation at UV or higher levels. What makes this possible is that quantum mechanics requires the specific heat of atoms at the nanoscale to vanish. See  http://www.nanoqed.org/ at “Nanofluids and Thin Films”, 2009.

Vanishing specific heat may be understood from the fact the thermal energy of the atom given by the Einstein-Hopf relation depends on wavelength under the constraint that only submicron (< 1 micron) wavelengths are allowed to “fit inside” nanostructures. But submicron wavelengths are only populated at temperatures greater than about 6000 K. At ambient temperature, therefore, the heat capacity of nanostructures is “frozen out”, and so absorbed EM energy cannot be conserved by an increase in temperature. Conservation may only proceed by the QED induced frequency up-conversion of absorbed EM energy to the fundamental resonance of the nanostructure. Heat conduction is negated because the prompt conservation of absorbed EM energy by QED emission is far faster than the time it takes for the phonons to respond. Ibid, at “QED induced heat transfer”, 2010.  

Discussion
The prompt conservation of absorbed EM energy by QED emission means conduction does not occur at the nanoscale, and therefore phonon explanations of reduced conductivity in thin films are meaningless. Indeed, bulk conductivity at the macroscale may be assumed valid at the nanoscale. Ibid

The thermal conductivity by TDTR measurements of submicron samples is only apparent. Conductivity appears reduced from that of bulk only because QED emission was excluded in the heat balances. If included, there is no conduction and bulk conductivity is still valid. What this means is that the a priori assumption may be made that absorbed EM energy of any form by a nanostructure is promptly emitted as QED radiation at UV or higher levels Hence, Molecular Dynamcis (MD) simulations to determine the response of the nanostructure to the absorbed EM energy are no longer necessary.The only relevant MD simulation might be the interaction of the QED emission with the surroundings.Ibid

Conclusions

1. The conclusion that size in terms of the sample thickness is not expected to make a significant difference in measured conductivity for the 80 micron and 200 nm samples is negated by the size effect of quantum mechanics.

2. Conductivity appears reduced in submicron samples because QED induced radiation was excluded in the heat balances. If included, there is no conduction, and therefore the sample may be considered to have bulk conductivity under the condition of no heat flow. In fact, both submicron and 80 micron samples have bulk thermal conductivity.

3. Conclusions that phonons with a mean free path of ~ 100 nm make a sizeable contribution to conductivity not only contradict the fact current theoretical methods based on phonons cannot explain the higher conductivity of the 80 micron sample. In fact, both are meaningless because there is no conductive heat flow at the nanoscale.

4. TDTR measurements are likely caused by QED induced photons and have nothing to do with phonons.

5. The response of nanostructures to absorbed EM energy need not be determined by MD simulations; the only relevant MD simulation might be the interaction of the QED emission with the surroundings.

Cancer is caused by disorganization of epithelial tissue and not by DNA mutations

Posted on by

Mutations in the genomes of the tumor cell long thought to cause cancer is negated by QED induced ionizing radiation produced   as the MMP-3 enzyme disorganizes the basement membrane of epithelial tissues

Background Epithelial tissue forming the outer layers of the skin protect exterior surface of the body, but also provide protection for hollow organs and glands including the breast, prostate, colon, and lung from body fluids.  Epithelial tissue is organized by a submicron thick < 100 nm basement membrane (BM) that provides the structural scaffold template for the extracellular matrix (ECM). Breakdown of the BM is associated with the spread of tumors, e.g., loss of integrity of the BM in mice is known to cause tumors. See http://www.lbl.gov/Science-Articles/Archive/LSD-cancer-f … 

Loss of integrity in the ECM is triggered by enzymes called matrix metalloproteinases (MMPs). Breast tumors in particular are known to have an increased amount of MMPs. Indeed, MMPs induce the epithelial-mesenchymal transition (EMT) that disorganize the BM and allows the dissociated epithelial tissue to move through the body. In breast cancer, EMT allows tumor cells more mobility to penetrate barriers like the walls of lymph and blood vessels, facilitating metastasis, e.g., the MMP-3 enzyme causes normal cells to produce a protein called Rac1b that is found only in cancers. Currently, Rac1b is thought to stimulate the production of highly reactive oxygen species (ROS) molecules leading to cancer by damaging the DNA. Ibid

Problem and Hypothesis
The problem with epithelial tissue as the source of DNA damage is that the protein Rac1b lacks a mechanism to produce energy of at least 5 eV from which the ROS of peroxide and hydroxyl radicals form to damage the DNA. The ROS can only be produced by ionizing radiation > 5 eV at ultraviolet (UV) levels or beyond. 

But what is the mechanism of ionizing radiation?

Certainly, there are no UV lasers in body fluids. The hypothesis may therefore be made that epithelial tissue during disorganization somehow emits low level ionizing radiation.

Emission of Ionizing Radiation by Submicron Entities
Cancer research is only beginning to recognize the remarkable fact that submicron entities present in body fluids emit low-level ionizing radiation. Over the past few decades, this fact has been supported by experimental evidence that shows submicron entities comprising nanoparticles (NPs) of natural and man-made materials cause DNA damage. Remarkably, the NPs alone – without lasers – somehow induce DNA damage in body fluids. See http://www.nanoqed.org/ at “DNA damage by NPs”, 2009 and  “DNA damage by signaling,” 2010.

QED induced EM radiation
Recently, the theory of QED induced EM radiation was proposed to explain the remarkable fact that NPs alone cause DNA damage. QED stands for quantum electrodynamics and EM for electromagnetic. Ibid. By this theory, quantum mechanics forbids atoms in submicron NPs to have specific heat. This may be understood from the fact the thermal energy of the atom given by the Einstein-Hopf relation depends on wavelength under the constraint that only wavelengths < 1 micron are allowed to “fit inside” submicron entities. But quantum mechanics only allows submicron wavelengths to be populated at temperatures greater than about 6000 K. At ambient temperature, therefore, the heat capacity of submicron entities is “frozen out”, and so NPs cannot conserve absorbed EM energy by an increase in temperature. Absent UV lasers, NPs in body fluids absorb EM energy from colliding water molecules. Conservation then proceeds by the QED induced frequency up-conversion of absorbed EM collision energy to the fundamental resonance of the NP.  Typically, ionizing QED radiation is emitted at UV or higher levels thereby explaining how NPs alone produce the ROS that damages DNA. Specifically, ionizing radiation > 5 eV necessary for forming ROS is produced for NPs < 100 nm. Ibid

Epithelial cell induced DNA damage
Epithelial tissue like NPs induce DNA damage provided submicron entities are produced upon disorganization by MMPs. QED induced radiation is emitted if the size of the biological entity is < 100 nm and has a refractive index greater than the surroundings. For biological materials, the index is about 1.5 > 1.33 for water. But epithelial cells themselves are not submicron and at 10-100 microns in the disorganized state do not emit ionizing radiation. However, ionizing radiation is emitted from the < 100 nm BM upon disorganization of epithelial tissue by MMPs.

By the theory of QED induced radiations, the disorganization of the BM by MMP-3 produces the ionizing radiation that forms the ROS that in turn damage the DNA. Current thought that the Rac1b protein itself damages the DNA is therefore placed in question. Indeed, the Rac1b protein is a cancer marker only because it forms in the process of ionizing radiation be produced by the disorganized BM. Nevertheless, Rac1b as a small protein is a submicron entity that once in the disorganized state like the BM also produces ionizing radiations that may damage surrounding DNA. See Press Release http://www.prlog.org/10793056-cancer-is-caused-by-disorganization-of-epithelial-tissue-and-not-by-dna-mutations.html

Conclusions

1. During disorganization by MMP-3, the BM emits QED induced ionizing radiation forming ROS that damage the DNA and produce the Rac1b protein found in most cancers.

2. Contrarily, the ROS are not induced by Rac1b to stimulate the development of cancer by directly affecting genomic DNA. Rather, the ROS are formed in a side reaction from the QED induced radiation emitted from the disorganized BM. Nevertheless, the Rac1b protein as a submicron entity is the product of the ROS and may also damage nearby DNA.

3. Loss of epithelial tissue organization produces QED induced EM radiation that damages the DNA before mutations occur in the genome of the tumor cell by other factors.

4. Oncogenes are activated by QED induced radiation from changes in the BM structure by MMPs.

5. UV absorptive drugs may be used to reduce QED induced radiation and attendant DNA damage from epithelial tissue disorganization by MMP-3.

The toxicity of colloidal silver and risk of cancer

Posted on by

Background

Scientific American in 2008 published an article entitled: Do Nanoparticles in Food Pose a Health Risk? The article reports the widespread use of nanoparticles (NPs) in food or food-related products that do not bear the warning that they may pose a health risk. The FDA does not require NPs to be proved safe, but rather requires the foods having NPs to not be harmful. In 2006, the EPA began to regulate nanosilver as a pesticide and as a result companies using nanosilver as an antimicrobial agent are required to register them as pesticides. Friends of the Earth, an environmental group, insist that reporting of nanosilver use by companies should be mandatory, given the potential risks and has suggested the definition of what constitutes a health risk to include NPs < 300 nm in diameter. But Andrew Maynard of the Woodrow Wilson International Center for Scholars notes it is the effect rather than the size that is significant. See http://www.scientificamerican.com/article.cfm?id=do-nanoparticles-in-food-pose-health-risk

Toxicity by Surface Area and Size

Currently, the mechanism by which NPs pose a health risk is not well understood. NP size controls the surface area and therefore the effectiveness of colloidal silver. NPs are thought to be more reactive than larger particles of the same substance, because they have more surface area and therefore have more opportunity to interact with other substances in their surroundings, i.e., a material that is otherwise harmless at the macroscale is likely to be toxic if it is processed to the nanoscale as NPs. See http://www.scientificamerican.com/article.cfm?id=will-nano-particles-present-big-health-problems The problem with quantifying toxicity by NP surface area and size is that both lack a mechanism to produce EM energy of at least 5 eV to form the reactive oxidative species (ROS) necessary to act as bactericidal agents. EM stands for electromagnetic. Similarly, the significance of “effect rather the size” in toxicity suggested by the Wilson Center lacks a mechanism to produce the ROS.

QED Induced EM Radiation Toxicity

More recently, the toxicity mechanism of NPs capable of producing ROS was proposed to find origin in quantum mechanics. Toxicity is found to almost be independent of the material, although silver has received the most attention because of its use as a bactericide in baby food. By this theory, atoms in NPs lack specific heat because at ambient temperature the heat capacity in submicron NPs resides at wavelengths < 1 micron that may only be populated at temperatures greater than about 6000 K. At ambient temperature, the heat capacity is therefore “frozen out”, and so NPs lack the heat capacity to conserve absorbed EM energy from colliding water molecules in body fluids by an increase in temperature. Conservation may only proceed by the QED induced frequency up-conversion of absorbed EM energy to the EM resonance of the NP. QED stands for quantum electrodynamics. Typically, ionizing QED radiation is emitted at UV or higher levels thereby producing the ROS that damage DNA from which cancer may develop. NPs < 100 nm are required to produce ROS through ionizing radiation. In contrast, NPs > 100 nm emit non-ionizing QED radiation in the VIS and IR. See http://www.nanoqed.org at “DNA damage by NPs”, 2010.

Colloidal Silver

Colloidal silver comprising silver NPs in solution is related to the controversy over the risks of silver NPs in food products. Colloidal silver has been used for fighting infections for thousands of years. But for the last 40 years, silver colloids have been proven to be cancer-causing agents. Indeed, silver is listed in the 1979 Registry of Toxic Effects as causing cancer in animals. Silver finds antibiotic action from the fact that it is a non-selective toxic biocide. See e.g., http://www.cqs.com/silver.htm  Regardless, fine silver NPs provide greater effectiveness than coarse NPs because toxicity is predicated on exposing the infected region to the largest possible surface area. See http://www.silver-colloids.com/Reports/reports.html#CompTable

 Safe Colloidal Silver?

Currently, comments to the Scientific American article stated if the widely touted “natural antibiotic” usage of colloidal silver is a potentially dangerous thing, then: Are there any safe colloidal silvers? Or Are the silver components in such preparations larger than problematic?  

Answers to these questions depend on effectiveness. Colloidal silver is perfectly safe if not taken at all, but is not effective if other antibiotic agents are not used. Least effective are silver colloids with coarse NPs > 100 nm because the QED radiation emitted by the NPs in the VIS and IR is non-ionizing. Most effective are fine NPs < 100 nm, but come at the risk of damaging the DNA by UV or higher ionizing radiation that can lead to cancer.

 Moreover, coarse NPs accompanied by fine NPs actually enhance the DNA damage above that by fine NPs alone. Hence, manufacturers would have to guarantee that all NPs in the colloidal silver are > 100 nm to avoid ionizing radiation. Manufacturers of colloidal silver would be required to label the minimum size of NPs in their products to allow the customer himself to weigh the risk of DNA damage to antibiotic effectiveness.  

 Conclusions

1. NPs by emitting QED induced ionizing radiation are significant antibiotic agents, but pose a health risk by collateral damage to DNA the consequence of which may lead to cancer. DNA damage must always be considered in the use of NPs as antibiotics.

2. All NP materials produce about the same QED radiation because their refractive indices are similar. Therefore, only the NP size distinguishes whether ionizing or non-ionizing is emitted. Labeling of the minimum size of NPs in a product allows the customer to weigh the respective advantages and disadvantages.

3. Colloidal silver with NPs < 100 nm produce ionizing QED radiation at UV or higher levels that damage the DNA and can lead to cancer even though being used for thousands of years.

4. Safe colloidal silver may be found at minimum effectiveness. If manufacturer control all NPs > 100 nm, non-ionizing QED radiation is then emitted.  Controlling NPs > 300 nm can only err on the safe side.

5. The safest way of avoiding future cancers caused by DNA damage is to ban all NPs < 300 nm from food products, especially baby food.

Materials At The Nanoscale Have Zero Specific Heat

Posted on by

 Background
Specific heat is thought to be an intensive thermophysical property independent of the amount of the substance. Given the amount of the substance in a body is proportional to its volume, specific heat should therefore be independent of whether the body dimensions are macroscopic or nanoscopic. In contrast, specific heat that depends on the amount of the substance is an extensive property dependent on the dimensions of the body.  See http://en.wikipedia.org/wiki/Specific_heat_capacity

 Classical Specific Heat at the Nanoscale  Currently, specific heat at the nanoscale is considered an intensive property having the same value as for macroscopic bodies. The Debye and Einstein macroscopic theories of specific heat including modifications thereof by Raman are generally assumed in simulating heat transfer in nanostructures. See Thumbnail of “Macroscopic Specific Heat at the Nanoscale?”. What this means is the classical oscillators of statistical mechanics from macroscopic bodies all having the same kT energy are used to model specific heat at the nanoscale. See Ibid.

Specific Heat by Quantum Mechanics Contrarily, quantum mechanics (QM) embodied in the Einstein-Hopf relation for the harmonic oscillator shows the QM states do not have the same kT energy at the nanoscale. At ambient temperature, the average Planck energy of QM states is kT only at thermal wavelengths greater than about 50 microns while at shorter wavelengths is less than kT and vanishes for nanostructures at submicron wavelengths.  See Paper and Presentation at “Zero Specific Heat”, http://www.nanoqed.org , 2010.

Since the Planck energy at a given wavelength is the amount of thermal energy that can be stored in the QM oscillator, and since the only thermal wavelengths that can fit into nanostructures are submicron, QM requires zero specific heat capacity at the nanoscale, the consequence of which is absorbed heat cannot be conserved in nanostructures by an increase in temperature. Conservation may only proceed by the QED induced frequency up-conversion of absorbed heat to non-thermal EM radiation at the fundamental EM confinement frequency of the nanostructure, typically in the UV and beyond. The EM confinement is quasi-bound allowing leakage of QED induced radiation from the nanostructure to be absorbed in the macroscopic surroundings. See Ibid.

But QED emission in the UV and beyond from nanostructures is not readily observed – even by standard photomultipliers because of the UV cut-off, and therefore heat balances of nanostructures do not include QED emissions as heat losses. Hence, thermal conductivity is inferred to be reduced from that of the bulk to be consistent with the measured temperature difference across the body, e.g., as in thin films. If QED emissions are included in heat losses, the bulk conductivity need not be reduced for consistency with temperature differences thereby precluding any modification of Fourier’s theory of heat conduction by the Boltzmann transport equation (BTE). See Ibid.  

 Molecular Dynamics and Periodic Boundaries  Molecular Dynamics (MD) describes the classical solution of atomic motion based on Newton’s equations. To determine bulk transport properties, there are no QM restrictions on kT energy of atoms, i.e., atoms are assumed to have kT energy because the MD solution for the bulk is obtained by imposing periodic boundary conditions on the computational box. Historically, Monte Carlo (MC) preceded MD simulations, however. MC simulations of spherical particles in a submicron computational square with periodic boundaries were used to determine the 2D virial coefficients for the PVT equation of state. See Metropolis et al. Ibid.For a discrete nanostructure, periodic boundaries do not apply, and therefore the atoms in the nanostructure are subject to QM restrictions of zero kT energy.

Heat transfer of discrete nanostructures which are unambiguously not periodic is generally simulated by MD on the invalid assumption the atoms have kT energy. See e.g., http://pubs.acs.org/doi/full/10.1021/ct7002594  Extending specific heat from macroscopic samples to the nanoscale is just as invalid as extending the Dulong-Petit law for specific heat at ambient temperature to low temperatures about 200 years ago. Nevertheless, MD simulations of nanostructures today are proudly displayed in the belief they provide precise atomistic explanations of conduction heat transfer when in fact they are not valid because the simulations are performed on the assumption the atoms have finite kT energy. See Ibid, and http://www.scienceblog.com/cms/blog/8209-quantum-mechanics-questions-molecular-dynamics-submicron-structures-25639.html

Conclusions

1. QM requires zero specific heat capacity at the nanoscale be specified as a new thermophysical property of all materials.

2. The classification of specific heat as an intensive thermophysical property of a body should be changed to an extensive property depending on the dimensions of the body.

3. Nanoscale heat transfer based on the assumption of macroscopic specific heat is likely to produce unphysical results, e.g., reduced thermal conductivity in thin films.

4.  There is no need for the BTE to determine the thermal conductivity in thin films as bulk conductivity may be assumed without any loss in accuracy.

5. Macroscopic Debye and Einstein theories should be revised to include zero specific heat at the nanoscale.

6. Lacking specific heat at the nanoscale, absorbed EM energy is not conserved by an increase in temperature, but rather by the emission of non-thermal QED induced EM radiation.

7. MD and MC simulations of bulk thermal conductivity based on full kT energy of atoms in submicron computational boxes under periodic boundary conditions are consistent with QM.

8. Zero specific heat is required for atoms in MD and MC simulations of discrete nanostructures without periodic constraints.

9. Absorbed EM energy in discrete nanostructures may be a priori assumed to be emitted as high frequency EM radiation that is absorbed in the macroscopic surroundings, thereby obviating any need to perform MD and MC simulations of the nanostructure itself.

Nanotrumpets Produce Sound from Joule Heat Without Temperature Fluctuations

Posted on by

Recent claims based on classical heat transfer that nanotrumpets produce sound from temperature fluctuations caused by Joule heating in passing electrical current through thin films are refuted by quantum mechanics.

Background
Recently, the journal Nature published an article entitled Nanotherm Trumpets that claimed sound was produced from temperature fluctuations in passing electrical current through an array of nanometer thick aluminum films. The claim is based on classical heat transfer theory that assumes films under Joule heating increase in temperature to heat the surrounding air and produce the pressure in propagating the sound. High thermal conductivity of the films is thought to allow the Joule heat to be lost to the substrate, and therefore not contribute to the large temperature fluctuations necessary to produce sound. To avoid loss of Joule heat, reductions in bulk thermal conductivity are viewed as an important feature of the Nanotrumpets. Required reductions in thin film thermal conductivity are supported by scattering of electrons in the Boltzmann transport equation (BTE). See “Nature Article” under http://www.nanoqed.org, “Thermophone” at “Nanotrumpet Update”, 2010.

Classical Heat and QM Transfer
Quantum mechanics (QM) trumps the classical heat transfer theory claims that sound is produced from temperature fluctuations in nanometer thick films. QM precludes any fluctuations in the film temperatures because the specific heat given by the heat capacity of the atom vanishes in submicron films, and therefore there can be no heat flow through the thin film. Without heat flow, bulk conductivity may be retained in temperature solutions by Fourier’s heat conduction theory yielding isothermal temperatures without gradients. Hence, there are no temperature fluctuations in the film to heat the surrounding air and produce sound. Conversely, sound by QM is produced without temperature fluctuations by conserving the Joule heat by the emission of non-thermal electromagnetic (EM) radiation from the surfaces of the thin film. Pressure fluctuations producing the sound are caused by the absorption of the EM radiation in the surrounding air. The validity of classical heat transfer theory in thin films having submicron thicknesses was the subject of an earlier critique of the BTE. See http://www.prlog.org/10321896-thermophones-produce-sound…

QED induced EM Radiation
In general, QM precludes nanostructures of any form from conserving absorbed EM energy by an increase in temperature. See http://www.nanoqed.org, 2009 and 2010. Instead, the absorbed EM energy is conserved by creating photons inside the nanostructure at its fundamental EM confinement frequency, the process called QED induced EM radiation. QED stands for quantum electrodynamics. The QED process is consistent with QM that asserts photons of wavelength L are spontaneously created upon supplying EM energy U to a QM box with walls separated by L/2. It is important to emphasize the QED photons are created inside the solid nanostructure where the velocity c of light is reduced by the refractive index n of the solid. For a thin film, the QED photons created in the thickness direction are under EM confinement at wavelength L = 2nT, where T is its thickness. The number N of QED photons created having Planck energy E is N = U/E, where E = hc/2nT and h is Planck’s constant. See Ibid.

With regard to the verification of QED radiations, the EM emission may be difficult to detect. Submicron thin films create QED photons having Planck energies in the ultraviolet (UV) and beyond, and therefore are beyond the typical cut-off of most photomultipliers. But verification is possible with thicker films, e.g., QED radiation in the near infrared (NIR) is emitted from films having supramicron thicknesses. Since Joule heat is typically low frequency EM radiation in the far infrared (FIR), thin films may be considered frequency up-conversion devices converting FIR to EM radiation from the NIR to the UV or beyond.

Comments on Nanotrumpet Claims

Reduced Conductivity Requirement The Nature article cites a recent paper by Niskanen et al. showing an array of 3 micron wide x 30 nm thick x 200 micron long aluminum wires (sic films) suspended above a silicon substrate by an air gap g of 1-2 microns. The claim that reducing the bulk conductivity Kal of aluminum is required to reduce heat loss to the substrate is unlikely because the air film insulates the film from the substrate. In fact, the thermal resistance R between the outer film surface and the substrate is the sum of R1 and R2, where R1 = T / Kal is the resistance of the thin aluminum film and R2 = g / Kair that of the air gap. For bulk aluminum and air, Kal = 240 W/mK wile air has Kair = 0.026 W/mK. The R1 and R2 resistances are then 1.25e-10 and 5e-5 sq-m K/W. Hence, the air gap and not the aluminum film limit the heat loss to the substrate. Even if the bulk conductivity of aluminum is reduced to 70W/mK as claimed by BTE theory, the resistance of the air film still controls the heat loss to the substrate. The conductivity of the thin film is therefore inconsequential to the sound produced by the Nanotrumpet.

BTE and Reduced Conductivity In support of the claim that the BTE reduces the bulk conductivity of aluminum, thereby reducing the heat loss to the substrate and enhancing the sound, the Nature article cites the BTE paper by Jin et al. that claims reductions in bulk conductivity of aluminum to 70 W/mK for a 30 nm thick film is close to that found in experiments. But this claim is unlikely because the reduced conductivities were computed based on an assumed 10K temperature difference across the thin film which is precluded by QM. Isothermally there is no temperature difference across the film, and therefore the BTE is consistent with QM by predicting no reduction in bulk conductivity. The BTE is therefore also inconsequential in producing sound from the Nanotrumpet.

Conclusions

1. Classical heat transfer that includes finite specific heat in thin films is not applicable to Nanotrumpets. Sound cannot be produced by temperature fluctuations that are precluded by QM.

2. Instead of producing temperature fluctuations, QM allows the Nanotrumpets to conserve the Joule heat by the emission of EM radiation that upon absorption in the surrounding air produces the sound.

Nanocars are powered by electrostatic forces from QED induced charges

Posted on by

Nanocars comprising fullerene spherical wheels on hydrocarbon axles are shown to move on substrates by electrostatic forces from charges produced by quantum electrodynamics (QED)

Background
Nanocars evolved from research that began over a decade ago. At the IBM Zurich Research Laboratory, synthetic molecules (S-molecules) on a metal substrate were moved in a controlled and repeatable manner by pushing them with the tip of a scanning tunneling microscope (STM). See http://domino.watson.ibm.com/comm/wwwr_thinkresearch.nsf … .

The S-molecules included an organic molecule called porphyrin comprising a ring of atoms about 1.5 nanometers in diameter with a metal atom at its center. Groups of hydrocarbons were added to the porphyrin to provide four leg supports. The function of the legs was thought to allow the S-molecule to grip the surface to stabilize random thermal motion. Friction between the legs and the substrate could not have been significant because upon nudging with the STM tip the S-molecules appeared as though they were on rollers.

Quantum Mechanics Explanation
The S-molecule motion may be explained by quantum mechanics (QM). The Einstein-Hopf relationship for the QM harmonic oscillator shows the thermal kT energy of an atom at ambient temperature resides in the far infrared (FIR) beyond 50 microns. Here, k is Boltzmann’s constant and T is absolute temperature. But the S-molecule by its size excludes all thermal radiation beyond a few nanometers, and therefore lacks the heat capacity to conserve the FIR heat absorbed from the contact of the legs with the substrate by an increase in temperature. Upon contact of the legs with the substrate, the S-molecule becomes a part of a macroscopic body that by QM is allowed to have kT energy. But in moving, the S-molecule breaks contact to be momentarily isolated from the substrate, and therefore has excess kT energy above the vanishing small amount allowed by QM.

Lacking heat capacity, the S-molecule cannot conserve the excess kT energy by an increase in temperature. Conservation therefore may only proceed by the QED induced frequency up-conversion of the excess kT energy in the FIR to the electromagnetic (EM) confinement frequency of the S-molecule, which at ultraviolet (UV) levels and beyond has the Planck energy to charge the S-molecule by the photoelectric effect.

The QED induced charge only produces momentary electrostatic interactions. Nevertheless, the S-molecule is held to the substrate by momentary electrostatic attraction instead of by gripping as initially thought. Lateral motion depends on the momentary electrostatic interaction with its neighbors. In a random arrangement of S-molecules, the electrostatic interactions are not symmetric and on that basis alone may initiate motion. Moreover, lateral motion over the substrate occurs by intermittent stick-slip, but small friction at contacts makes it appear as though the S-molecule is on rollers. Regardless, contact neutralizes the charge on the S-molecule and allows the kT energy to be reacquired from the substrate to allow subsequent breaking of contact to produce QED charge. During stick-slip motion, the intermittent QED induced charge occurs very rapidly and may be difficult to detect.

Nanocars
Today, nanocars moving on substrates are more complex than the S-molecules, but the QED charging is the same. Currently, many research groups are engaged in nanocar research typified by Rice University. See http://news.cnet.com/Here-come-the-nanocars/2100-11395_3 ….

In QED charging, nanocars like S-molecules are powered by converting EM energy into mechanical motion. The EM energy may take various forms of heating including light, thermal, Joule, and electron beams. Indeed, nanocars have been shown to move by simply heating the substrate, the form of heat being the same thermal kT energy driving the earlier S-molecules. In effect, nanocars act as FIR to higher frequency up-conversion devices that charge the nanocars by producing momentary electrostatic repulsive forces that produce the observed nanocar motions. Similar arguments allow QED charges to explain the motions of molecular motors under Joule and electron beam heating. See http://www.nanoqed.org at “Nanocars by Quantum Mechanics”, 2010.

Molecular Dynamics
Unfortunately, the QED charging by which thermal kT energy is converted into powering the nanocar is not included in a conventional MD solution that implicitly assumes atoms have kT energy at the nanoscale. Valid MD simulations in heat transfer need to specify vanishing kT energy in the MD computational algorithms, and if so included would give isothermal temperature solutions. The invalidity of MD in heat transfer at the nanoscale is widespread, e.g., in tribology, see http://www.scienceblog.com/cms/blog/8209-quantum-mechanics-questions-molecular-dynamics-submicron-structures-25639.html ; whereas, in nanocars, see http://pubs.acs.org/doi/full/10.1021/ct7002594

MD is not needed for heat transfer at the nanoscale because temperature solutions are, a priori known to be isothermal. However, QED induced charging in nanostructures can and should be included in MD simulations of dynamic response, at least within the restrictions of Newton’s equations.

Conclusions

1. Nanostructures including S-molecules, nanocars, CNT motors and the like act as frequency up-conversion devices that are charged from QED radiation by the photoelectric effect, thereby allowing pair-wise interactions by momentary electrostatic repulsion.

2. MD simulations of heat transfer in nanocars are precluded by QM. At ambient temperature, the thermal heat capacity resides in the FIR beyond 50 microns, and therefore nanocars by their size exclude the heat capacity necessary for heat transfer. MD simulations of heat transfer in nanostructures are simply meaningless.

3. Unlike heat transfer, MD simulations are valid if directed to deriving the dynamic response of nanostructures on substrates under momentary QED induced charges.

Quantum Mechanics In Submicron Thin Metal Films Allows Conversion of the Full Solar Spectrum To Electricity

Posted on by

Quantum mechanics allows heat absorbed in submicron thin metal films over the full solar spectrum to be converted to electrical current by the photoelectric effect.

Background
In 1901, Nikola Tesla described the photoelectric effect in US patent “Apparatus for the Utilization of Radiant Energy.” Charging was accomplished by using a metal plate exposed to ultraviolet (UV) radiation. If applied to solar cells, a polished insulated metal plate will gain a positive charge as electrons ejected from the UV content in sunlight are continually drained to a capacitor. See http://en.wikipedia.org/wiki/Photoelectric_effect In his patent, Tesla noted that as the radiation falls on the metal plate, the capacitor will charge indefinitely. One of Tesla’s many US and Foreign patents is shown below.

Today, solar cells are generally not based on Tesla’s photoelectric effect. Instead, the photovoltaic (PV) effect is used where lower intensity visible (VIS) light moves electrons out of the valence band of semiconductors into higher-energy conduction bands, thereby producing electric current at a voltage related to the band-gap energy. But with PV’s made from single crystal or multi crystal semiconductors, the materials comprise up to 40% of the unit cost. Because of this, PV solar cells comprising very thin films of amorphous silicon or copper indium gallium selenide (CIGS) are of great interest because the thin films allow many more cells to be made with the same material, thereby significantly lowering costs. But unlike Tesla’s metal plate that absorbs almost all VIS and UV radiation, semiconductor and CIGS at thin film thicknesses lack the absorption necessary to efficiently capture the full solar spectrm. Organic PV cells now being considered in thin film technology are limited to thicknesses of about 3 microns. See Hong Kong Winter School on Solar Cells at http://physics.hkbu.edu.hk/home/Winterschool.html

Moreover, thin film PV cells are usually limited to the VIS part of the solar spectrum. Infrared (IR) light with a wavelength between 0.7 and 300 microns cannot be utilized in PV cells by moving electrons between the valence and conduction bands or by ejecting electrons from metals by Tesla’s photoelectric effect. Nevertheless, IR light comprises a large fraction of sunlight that is lost in the PV solar cells. At sea level, bright sunlight provides about 1000 watts per square meter at sea level. Of this, 527 watts is IR with 445 and 32 watts per square meter in the VIS and UV, respectively.

Submicron Thin Metal Films
Thin film PV technology based on silicon, CIGS, and organic materials is conceptually limited because solar radiation cannot be efficiently absorbed in thicknesses less than about 3 microns. However, thin metal films absorb from the UV to the IR even at submicron thicknesses. In effect, all solar radiation is absorbed in metals, but in thicknesses of a more than a few microns is converted to heat. Neither PV’s or Tesla’s photoelectric effect convert heat to electricity, and therefore another mechanism is required to allow thin metal films to efficiently function at solar cells.

QED Induced Radiation
QED induced radiation allows heat absorbed in thin metal films over the full solar spectrum to be converted to electricity. Here QED stands for quantum electrodynamics. In effect, Tesla’s photoelectric effect is extended to submicron thin film technology. How heat absorbed is converted to electrical current can be understood by quantum mechanics

Classically, heat is transferred by convection, radiation, and conduction, but in thin films is restricted by quantum mechanics to vanishing heat capacity in the thickness direction. Although the specific heat remains at macroscopic values in the in-plane directions, this is inconsequential because there is little if any in-plane temperature changes. See http://www.nanoqed.org/ at “Nanofluids and Thin Films”, 2009.

Quantum Mechanics Restrictions
The quantum mechanics restriction is described in the Einstein-Hopf relation for the harmonic oscillator that shows the average Planck energy of an atom at temperature is dispersed with wavelength. At room temperature, the thermal kT energy of the oscillator rapidly vanishes below wavelengths of about 50 microns, and therefore submicron thin films lack heat capacity because their thickness excludes all thermal wavelengths beyond about 1 micron. Here k is Boltzmann’s constant and T absolute temperature. What this means is all solar radiation irrespective of its wavelength that is absorbed in submicron thin films cannot be conserved by an increase in temperature.

Conservation of absorbed Solar Radiation
Nevertheless, the absorbed heat must be conserved. Typically, submicron thin films have EM confinement frequencies in the thickness direction beyond the UV. Here EM stands for electromagnetic. Since heat is low frequency EM energy, conservation may proceed by inducing the heat by QED to be frequency up-converted to levels beyond the UV. In effect, submicron thin films act as frequency up-conversion devices converting VIS and IR solar radiation to UV radiation that has the Planck energy that charges the film by Tesla’s photoelectric effect. In contrast, thin metal films having thicknesses greater than a few microns increase in temperature upon absorbing solar radiation and are inconsequential in solar energy conversion.

Conclusions

1. Thin film technology in PV solar cells is conceptually limited because silicon, CIGS, and organic materials lack the absorption of solar radiation at thicknesses less than about 3 microns.

2. Metal thin films regardless of thickness allow absorption of solar radiation from the UV through the VIS to the IR.

3. Thin metal films having thicknesses greater than a few microns increase in temperature upon the absorption of solar radiation. But in submicron thin films, quantum mechanics precludes the conservation of absorbed solar radiation by an increase in temperature.

4. Conservation of absorbed solar energy in submicron thin metal films may only proceed by QED induced frequency up-conversion to the EM confinement frequency of the thin film in the thickness direction, the latter in the UV and beyond.

5. Thin metal films induce the QED up-conversion of absorbed VIS and IR radiation to UV levels and beyond necessary to free electrons and charge the thin metal film. Without QED induced radiation, the VIS and IR lack the Planck energy to free electrons and produce electrical current.

6. The consequence of QED induced radiation is that submicron thin metal films by Tesla’s photoelectric effect offer the possibility of utilizing the full solar spectrum to produce electrical current.

Quantum Mechanics Questions the Molecular Dynamics of Submicron Structures

Posted on by

In the 1950s, Metropolis and Teller pioneered molecular dynamics (MD) as a method to derive the thermodynamic and transport properties of bulk molecular liquids. Submicron ensembles comprising a few hundred atoms with periodic boundary conditions were used to derive the bulk liquid properties. Even though the ensembles were submicron, the periodic boundary conditions allowed the heat capacity of the atom at wavelengths longer than the dimensions of the ensemble to be included in the MD simulations.

Today, MD simulations have been extended almost entirely to discrete submicron structures. See WTC IV The implicit assumption in the later MD simulations was there is no difference between the thermal heat capacity of the atoms in the discrete submicron structures and those ensembles in MD simulations with periodic boundary conditions.

However, quantum mechanics (QM) as embodied in the Einstein-Hopf relation shows the thermal heat capacity of the atom as given by the Planck energy of the harmonic oscillator depends on dispersion with wavelength. At ambient temperature, most of the thermal heat capacity of the atom is available at wavelengths > 100 microns where the thermal kT energy is about 25.8 meV. But the thermal emission from atoms in submicron structures is confined to wavelengths < 1 micron, and therefore excludes almost all of the heat capacity of the atom. Alternatively, atoms in discrete submicron structures in MD simulations lack the heat capacity necessary to conserve absorbed EM energy by an increase in temperature.

MD simulations of discrete submicron ensembles may proceed as usual provided the QM restriction on the heat capacity of the atoms is properly simulated. One such method is the theory of QED induced radiations. See QED radiations Lacking the heat capacity to conserve absorbed EM energy by an increase in temperature, the absorbed EM energy is frequency up or down-converted by QED to the EM confinement frequency of the submicron structure. Subsequently, the absorbed EM energy is conserved by the emission of non-thermal EM radiation.